バイオレゾナンス理論におけるNK細胞と病原菌の関係性

この図は、バイオレゾナンス理論におけるNK細胞と病原菌の関係性を示しています。図中の各ノードとエッジは以下のような関係を表しています:
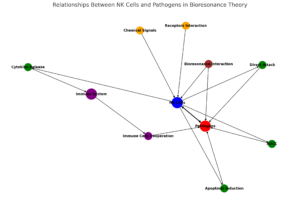
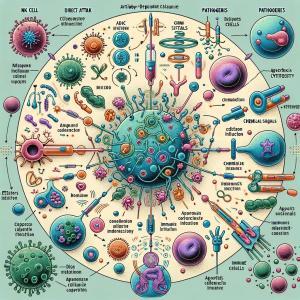
NK細胞が病原菌に対して効果的に作用するためには、単なる周波数の高さだけではなく、免疫システムの複雑な相互作用、化学信号、細胞間のコミュニケーションなどが非常に重要です。
バイオリゾナンス理論における周波数発生装置(例えばRife Machine)で癌細胞をターゲットにする方法については、いくつかの方法があります。以下に、その主要な方法を紹介します:
1. 同じ周波数で共振させる方法
癌細胞が共振する特定の周波数(42〜52 Hz)を利用して、これと同じ周波数を発生させ、癌細胞を共振させることにより細胞を破壊する方法。この方法は「共振破壊」として知られており、以下のように処理されます:
癌細胞の自然共振周波数を測定する。
同じ周波数を外部から与えることで、癌細胞を共振させ、細胞膜を破壊する。
共振により細胞が壊れ、癌細胞が死滅する。
2. 高い周波数で打ち消す方法
共振周波数よりも高い周波数を使用して癌細胞の活動を阻害する方法。この方法は癌細胞の成長や分裂を抑制するために用いられます。
癌細胞の共振周波数帯(42〜52 Hz)よりも高い周波数を使用。
高周波数により、癌細胞の機能や成長プロセスを妨害。
癌細胞の生存や増殖が抑制される。
具体例
これらの方法をシミュレートするために、以下のような仮設を立ててみます:
同じ周波数で共振させる場合
/*
================================================================================
【プログラム名】resonance_sim.c
【位置づけ・免責】
・本コードは「バイオレゾナンス」等で語られる考え方を“数値的にたとえる”
ための可視化モデルです。
・臨床効果や診断精度を保証するものではありません。
【事実と仮説の整理】
〈事実〉
– 生体は多因子相互作用系。NK細胞の直接傷害/ADCC/サイトカインなどは
免疫学の標準的知見。
– EEG α波(8–12 Hz)は脳の電気活動として実在するリズムだが、
“臓器の固有共鳴”とは異なる概念。
– TTFields(数十〜数百kHz帯)は腫瘍分裂過程を妨げる電場治療として
一部適応で臨床実装。低周波の臓器共鳴とは機序も帯域も別。
〈仮説/未検証〉
– 臓器や癌が特定の低周波で共鳴し、外部周波数で破壊/抑制できるという主張。
– 臓器ごとの固定“周波数リスト”の臨床的有効性。
– 「高周波で低周波を打ち消す」一般原理の生体適用。
– NLS/Rife機器の疾患スキャン/治療効果の臨床的裏づけ。
【このモデルの数理(信号処理上の比喩)】
・標的周波数 f0 に対する応答をガウス関数で近似:
R_single(f; f0) = exp( – (f – f0)^2 / (2 * sigma^2) )
ここで sigma = f0 / 20(経験的設定)。
・標的帯域 [Fmin, Fmax] を等分し、それぞれの応答を総和:
R_total(f) = Σ_j R_single(f; f0_j)
・周波数は 10–100 Hz、標的帯域は例として 42–52 Hz(仮定値)を用いる。
【出力/使い方】
– resonance_data.txt に f vs 応答を出力
– gnuplot があれば赤帯(42–52 Hz)とともに表示
– ビルド: gcc resonance_sim.c -lm -o resonance_sim
– 実行: ./resonance_sim (Windowsは .exe)
================================================================================
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define N_POINTS 1000
#define FREQ_MIN 10.0
#define FREQ_MAX 100.0
#define TARGET_MIN 42.0
#define TARGET_MAX 52.0
/* ガウス応答を重ね合わせた概念上の“合成応答”を計算 */
void resonance_response(const double *frequency, const double *target_range,
int n_points, double *response) {
for (int i = 0; i < n_points; i++) {
double f = frequency[i];
double sum = 0.0;
for (int j = 0; j < n_points; j++) {
double f0 = target_range[j];
double sigma = f0 / 20.0; /* 経験的帯域幅(比喩的設定) */
double d = f – f0;
sum += exp( -(d*d) / (2.0 * sigma * sigma) );
}
response[i] = sum;
}
}
int main(void) {
double frequency[N_POINTS];
double target_range[N_POINTS];
double response[N_POINTS];
/* 周波数軸・標的帯域(いずれも仮定値) */
for (int i = 0; i < N_POINTS; i++) {
frequency[i] = FREQ_MIN + (FREQ_MAX – FREQ_MIN) * i / (N_POINTS – 1);
target_range[i] = TARGET_MIN + (TARGET_MAX – TARGET_MIN) * i / (N_POINTS – 1);
}
/* 合成応答を計算(概念モデル) */
resonance_response(frequency, target_range, N_POINTS, response);
/* 出力 */
FILE *fp = fopen(“resonance_data.txt”, “w”);
if (!fp) { perror(“resonance_data.txt open failed”); return 1; }
for (int i = 0; i < N_POINTS; i++) fprintf(fp, “%lf\t%lf\n”, frequency[i], response[i]);
fclose(fp);
/* gnuplot で可視化(なければスキップ) */
FILE *gp = popen(“gnuplot -persist”, “w”);
if (gp) {
fprintf(gp, “set title ‘Conceptual Resonance (Gaussian Superposition)’\n”);
fprintf(gp, “set xlabel ‘Frequency (Hz)’\n”);
fprintf(gp, “set ylabel ‘Response (arbitrary)’\n”);
fprintf(gp, “set grid\n”);
fprintf(gp, “set style fill transparent solid 0.3\n”);
fprintf(gp, “set object 1 rect from %lf, graph 0 to %lf, graph 1 fc rgb ‘red’\n”,
TARGET_MIN, TARGET_MAX);
fprintf(gp, “plot ‘resonance_data.txt’ with lines lw 2 title ‘Sum of Gaussians’\n”);
pclose(gp);
} else {
fprintf(stderr, “[info] gnuplot not found. Plot resonance_data.txt manually.\n”);
}
return 0;
}
/*
================================================================================
【プログラム名】highfreq_sim.c
【位置づけ・免責】
・高周波(例: 880 Hz)を中心としたガウス応答を、低周波横軸上
(10–100 Hz)に可視化するだけの概念モデルです。
・“高周波で低周波を打ち消す”といった生体一般原理を主張しません。
【事実と仮説の整理】
〈事実〉
– 生体電場治療としてはTTFieldsのようにkHz帯で分裂過程を妨げる方法がある。
低周波の“臓器共鳴”とは機序・帯域が異なる。
〈仮説/未検証〉
– 高周波が低周波を打ち消す一般原理の生体適用。
– 臓器・病変の固定周波数リストの臨床的有効性。
【このモデルの数理(比喩)】
・中心周波数 fH のガウス応答:
R_high(f; fH) = exp( – (f – fH)^2 / (2 * sigma^2) )
sigma = fH / 10(経験的設定)。
・表示の都合上、横軸は 10–100 Hz とし、fH が軸外にある場合は
“裾”だけが見える。
【出力/使い方】
– highfreq_data.txt に f vs 応答を出力
– gnuplot があれば赤帯(42–52 Hz)とともに表示
– ビルド: gcc highfreq_sim.c -lm -o highfreq_sim
– 実行: ./highfreq_sim (Windowsは .exe)
================================================================================
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define N_POINTS 1000
#define FREQ_MIN 10.0
#define FREQ_MAX 100.0
#define TARGET_MIN 42.0
#define TARGET_MAX 52.0
#define HIGH_FREQ 880.0
/* 高周波中心のガウス応答を計算(概念モデル) */
void high_frequency_response(const double *frequency, double high_freq,
int n_points, double *response) {
double sigma = high_freq / 10.0; /* 経験的設定(比喩) */
double denom = 2.0 * sigma * sigma;
for (int i = 0; i < n_points; i++) {
double d = frequency[i] – high_freq;
response[i] = exp( -(d*d) / denom );
}
}
int main(void) {
double frequency[N_POINTS];
double response[N_POINTS];
/* 可視化用の横軸(10–100 Hz) */
for (int i = 0; i < N_POINTS; i++) {
frequency[i] = FREQ_MIN + (FREQ_MAX – FREQ_MIN) * i / (N_POINTS – 1);
}
/* 高周波中心応答を計算(概念モデル) */
high_frequency_response(frequency, HIGH_FREQ, N_POINTS, response);
/* 出力 */
FILE *fp = fopen(“highfreq_data.txt”, “w”);
if (!fp) { perror(“highfreq_data.txt open failed”); return 1; }
for (int i = 0; i < N_POINTS; i++) fprintf(fp, “%lf\t%lf\n”, frequency[i], response[i]);
fclose(fp);
/* gnuplot で可視化(なければスキップ) */
FILE *gp = popen(“gnuplot -persist”, “w”);
if (gp) {
fprintf(gp, “set title ‘Conceptual High-Frequency-Centered Response (880 Hz)’\n”);
fprintf(gp, “set xlabel ‘Frequency (Hz)’\n”);
fprintf(gp, “set ylabel ‘Response (arbitrary)’\n”);
fprintf(gp, “set grid\n”);
fprintf(gp, “set style fill transparent solid 0.3\n”);
fprintf(gp, “set object 1 rect from %lf, graph 0 to %lf, graph 1 fc rgb ‘red’\n”,
TARGET_MIN, TARGET_MAX);
fprintf(gp, “plot ‘highfreq_data.txt’ with lines lw 2 lc rgb ‘orange’ ”
“title ‘Gaussian Tail (center=880 Hz)’\n”);
pclose(gp);
} else {
fprintf(stderr, “[info] gnuplot not found. Plot highfreq_data.txt manually.\n”);
}
return 0;
}
仮設のまとめ
同じ周波数で共振させる方法は、癌細胞の自然共振周波数を利用して細胞を破壊することを目的とします。
高い周波数で打ち消す方法は、癌細胞の成長や分裂を妨害することを目的とします。
実際のバイオリゾナンス治療においてどちらの方法が効果的であるかは、科学的な検証が必要です。